Introduction
A Binary Search Tree (BST) is a special type of Binary Tree where:
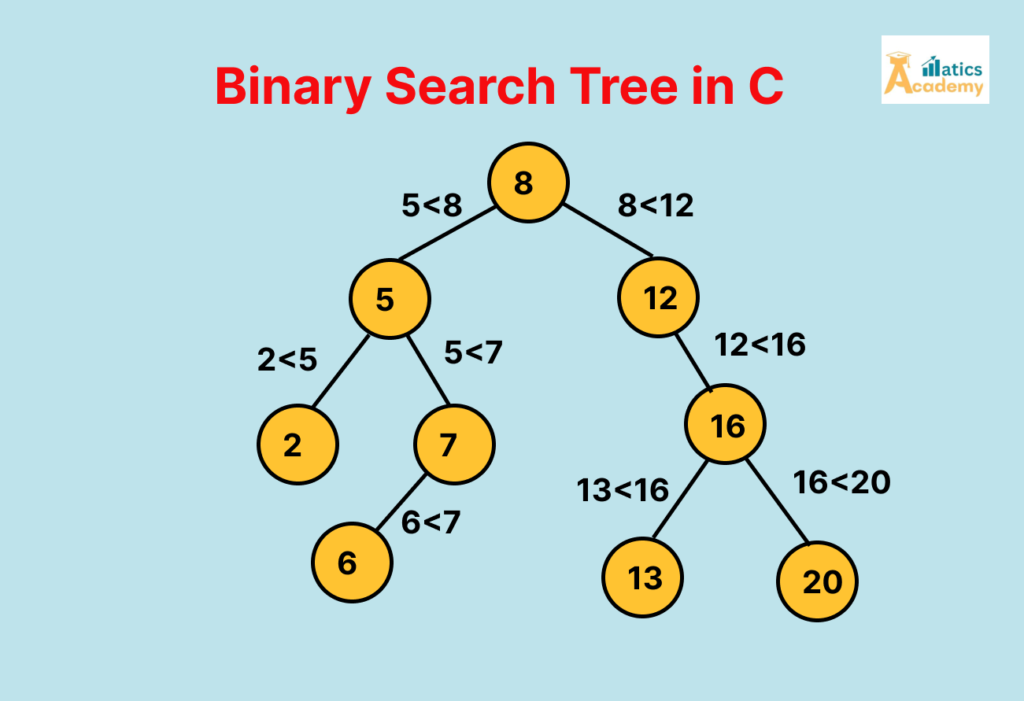
- The left child contains values smaller than the parent node.
- The right child contains values greater than the parent node.
- No duplicate values are allowed.
BSTs are widely used in search applications because they provide an average-case O(log N) search time.
Why Use Binary Search Tree?
- Fast Searching – O(log N) average-case time complexity.
- Efficient Insertion & Deletion – O(log N) in a balanced tree.
- Sorted Data Representation – Inorder traversal of BST gives elements in sorted order.
- Widely Used in Applications – Used in databases, file systems, and auto-suggestions.
Binary Search Tree Operations
- Insertion – Insert a new node while maintaining BST properties.
- Deletion – Remove a node and adjust the tree accordingly.
- Searching – Find an element efficiently.
- Traversal – Visit all nodes in different orders.
- Finding Min/Max – Get the smallest or largest element.
Binary Search Tree Implementation in C
Node Structure
Each node contains:
- Data
- Pointer to Left Child
- Pointer to Right Child
#include <stdio.h>
#include <stdlib.h>
// Define a structure for a BST Node
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// Create a new node
struct Node* createNode(int value) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
newNode->data = value;
newNode->left = newNode->right = NULL;
return newNode;
}
Insertion in Binary Search Tree
To insert a value:
- If the tree is empty, create a new node.
- If the value is less than the current node, go left.
- If the value is greater, go right.
struct Node* insert(struct Node* root, int value) {
if (root == NULL) return createNode(value);
if (value < root->data)
root->left = insert(root->left, value);
else if (value > root->data)
root->right = insert(root->right, value);
return root;
}
Insertion takes O(log N) time in a balanced BST.
Searching in Binary Search Tree
To search for a value:
- If the value matches the node, return it.
- If the value is smaller, search the left subtree.
- If the value is larger, search the right subtree.
struct Node* search(struct Node* root, int key) {
if (root == NULL || root->data == key)
return root;
if (key < root->data)
return search(root->left, key);
return search(root->right, key);
}
Search is O(log N) in a balanced BST.
Inorder Traversal (Sorted Output)
Inorder traversal (Left → Root → Right) prints elements in ascending order.
void inorder(struct Node* root) {
if (root) {
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
This is used to retrieve sorted elements from a BST.
Deletion in Binary Search Tree
To delete a node:
- Case 1: Node is a leaf – Delete it directly.
- Case 2: Node has one child – Replace it with its child.
- Case 3: Node has two children – Find the inorder successor (smallest in the right subtree) and replace the node with it.
struct Node* findMin(struct Node* root) {
while (root->left != NULL)
root = root->left;
return root;
}
struct Node* deleteNode(struct Node* root, int key) {
if (root == NULL) return root;
if (key < root->data)
root->left = deleteNode(root->left, key);
else if (key > root->data)
root->right = deleteNode(root->right, key);
else {
// Case 1: Node with only one child or no child
if (root->left == NULL) {
struct Node* temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct Node* temp = root->left;
free(root);
return temp;
}
// Case 2: Node with two children, find inorder successor
struct Node* temp = findMin(root->right);
root->data = temp->data;
root->right = deleteNode(root->right, temp->data);
}
return root;
}
Deletion takes O(log N) in a balanced BST.
Complete BST Implementation
#include <stdio.h>
#include <stdlib.h>
// Define structure for BST Node
struct Node {
int data;
struct Node* left;
struct Node* right;
};
// Create a new node
struct Node* createNode(int value) {
struct Node* newNode = (struct Node*)malloc(sizeof(struct Node));
if (newNode == NULL) {
printf("Memory allocation failed!\n");
exit(1);
}
newNode->data = value;
newNode->left = newNode->right = NULL;
return newNode;
}
// Insert a node in BST
struct Node* insert(struct Node* root, int value) {
if (root == NULL) {
return createNode(value);
}
if (value < root->data)
root->left = insert(root->left, value);
else if (value > root->data)
root->right = insert(root->right, value);
return root;
}
// Search for a value in BST
struct Node* search(struct Node* root, int key) {
if (root == NULL || root->data == key)
return root;
if (key < root->data)
return search(root->left, key);
return search(root->right, key);
}
// Find minimum value node
struct Node* findMin(struct Node* root) {
while (root && root->left != NULL)
root = root->left;
return root;
}
// Find maximum value node
struct Node* findMax(struct Node* root) {
while (root && root->right != NULL)
root = root->right;
return root;
}
// Delete a node from BST
struct Node* deleteNode(struct Node* root, int key) {
if (root == NULL)
return root;
if (key < root->data)
root->left = deleteNode(root->left, key);
else if (key > root->data)
root->right = deleteNode(root->right, key);
else {
// Case 1: Node with only one child or no child
if (root->left == NULL) {
struct Node* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
struct Node* temp = root->left;
free(root);
return temp;
}
// Case 2: Node with two children
struct Node* temp = findMin(root->right); // Find inorder successor
root->data = temp->data;
root->right = deleteNode(root->right, temp->data);
}
return root;
}
// Inorder Traversal (Left -> Root -> Right)
void inorder(struct Node* root) {
if (root != NULL) {
inorder(root->left);
printf("%d ", root->data);
inorder(root->right);
}
}
// Preorder Traversal (Root -> Left -> Right)
void preorder(struct Node* root) {
if (root != NULL) {
printf("%d ", root->data);
preorder(root->left);
preorder(root->right);
}
}
// Postorder Traversal (Left -> Right -> Root)
void postorder(struct Node* root) {
if (root != NULL) {
postorder(root->left);
postorder(root->right);
printf("%d ", root->data);
}
}
// Main function
int main() {
struct Node* root = NULL;
// Insert values into BST
root = insert(root, 50);
insert(root, 30);
insert(root, 70);
insert(root, 20);
insert(root, 40);
insert(root, 60);
insert(root, 80);
printf("Inorder Traversal: ");
inorder(root);
printf("\n");
printf("Preorder Traversal: ");
preorder(root);
printf("\n");
printf("Postorder Traversal: ");
postorder(root);
printf("\n");
// Search for a value
int searchValue = 40;
if (search(root, searchValue))
printf("Element %d found in BST.\n", searchValue);
else
printf("Element %d not found in BST.\n", searchValue);
// Find minimum and maximum
struct Node* minNode = findMin(root);
struct Node* maxNode = findMax(root);
if (minNode) printf("Minimum value in BST: %d\n", minNode->data);
if (maxNode) printf("Maximum value in BST: %d\n", maxNode->data);
// Delete a node
int deleteValue = 30;
printf("Deleting %d...\n", deleteValue);
root = deleteNode(root, deleteValue);
printf("Inorder Traversal after deletion: ");
inorder(root);
printf("\n");
return 0;
}
Output Click me!
Inorder Traversal: 20 30 40 50 60 70 80
Preorder Traversal: 50 30 20 40 70 60 80
Postorder Traversal: 20 40 30 60 80 70 50
Element 40 found in BST.
Minimum value in BST: 20
Maximum value in BST: 80
Deleting 30...
Inorder Traversal after deletion: 20 40 50 60 70 80
BST Applications
- Databases – Used in indexing and search optimization.
- File Systems – Directory structure follows a tree-based format.
- Auto-Suggestions – Used in predictive text and search engines.
- Symbol Tables – Used in compilers for variable/function lookups.
- Networking – Routing tables in networking use BST principles.
BST vs Other Data Structures
| Feature | BST | Array | Linked List |
|---|---|---|---|
| Search Time | O(log N) | O(N) | O(N) |
| Insert/Delete | O(log N) | O(N) | O(1) |
| Ordered Data? | Yes | No | No |
| Sorted Output | Yes | No | No |
BST is better than Arrays & Linked Lists for ordered data operations.
Conclusion
A Binary Search Tree (BST) is a powerful data structure for fast searching, insertion, and deletion operations. Understanding BSTs is essential for coding interviews and real-world applications like databases, search engines, and file systems.
Interview Questions
1. How do you insert a node into a Binary Search Tree (BST)?
Company: Google
Answer:
- If the tree is empty, create a new node as the root.
- If the value is smaller than the root, insert it into the left subtree.
- If the value is greater than the root, insert it into the right subtree.
. How do you find the minimum and maximum values in a BST?
Company: Amazon
Answer:
- The minimum value is found by moving to the leftmost node.
- The maximum value is found by moving to the rightmost node.
3. How do you delete a node from a BST?
Company: Microsoft
Answer:
- Case 1: If the node has no children, simply remove it.
- Case 2: If the node has one child, replace it with its child.
- Case 3: If the node has two children, replace it with its in-order successor (smallest value in the right subtree).
4. What is the difference between BST and AVL Tree?
Company: Meta (Facebook)
Answer:
| Feature | BST | AVL Tree |
|---|---|---|
| Balancing | Not guaranteed | Always balanced |
| Search Time | O(n) in worst case | O(log n) always |
| Rotations | No rotations required | Requires rotations after insertion/deletion |
| Performance | Can degrade to linked list in unbalanced cases | Ensures efficient search |
5. How do you check if a given tree is a BST?
Company: IBM
Answer:
To check if a tree is a Binary Search Tree (BST):
- Inorder Traversal Method:
- Perform an inorder traversal (left → root → right).
- If the values appear in ascending order, then it is a BST.
- Recursive Method:
- Check if each node follows the BST rule:
- Left child < Parent < Right child
- Recursively check the left and right subtrees.
- Check if each node follows the BST rule:
Quizzes
Binary Search Tree (BST) in C Quiz
