Recursion in Python is a cornerstone concept in programming, enabling developers to solve problems by breaking them into smaller, more manageable parts. In Python, recursion is both intuitive and powerful. Whether you’re preparing for interviews or looking to deepen your Python knowledge, this guide has you covered.
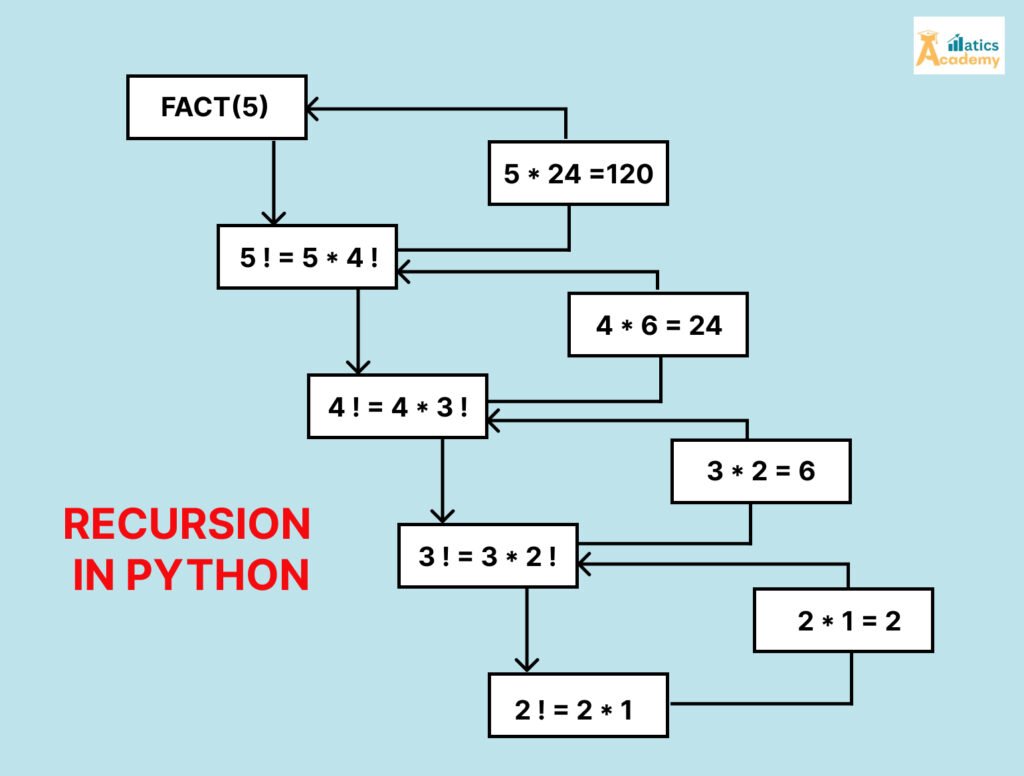
What is Recursion in Python?
Recursion occurs when a function calls itself to solve a problem. This technique is especially useful for tasks that can be divided into similar sub tasks.
Key Components of Recursion in Python:
- Base Case: A condition that terminates the recursion.
- Recursive Case: The function continues calling itself with modified parameters.
- Why Learn Recursion?
- Recursion is widely used in programming for its ability to simplify complex problems. Applications include:
- Mathematical Computations: Factorials, Fibonacci sequences, etc.
- Data Structures: Traversing trees and graphs.
- Problem Solving: Tower of Hanoi, maze-solving algorithms.
Why Use Recursion in Python?
Recursion is particularly useful for problems involving repetitive tasks or problems that can be divided into smaller, similar tasks, such as:
- Mathematical computations (e.g., factorial, Fibonacci sequence).
- Data structure traversal (e.g., trees and graphs).
- Solving puzzles (e.g., Tower of Hanoi).
How Recursion Works in Python
Python handles recursion like any other function, but with a set recursion limit to avoid infinite loops.
import sys print(sys.getrecursionlimit()) # Default is 1000 sys.setrecursionlimit(1500) # Customize the limit as needed
Structure of a Recursive Function
def recursive_function(parameters):
if base_case_condition:
return base_case_value # Base Case
else:
return recursive_function(modified_parameters) # Recursive Case
Practical Examples of Recursion in Python
1. Factorial of a Number
def factorial(n):
if n == 0 or n == 1:
return 1 # Base Case
return n * factorial(n - 1) # Recursive Case
print(factorial(5)) # Output: 120
2.Fibonacci Sequence
def fibonacci(n):
if n == 0:
return 0 # Base Case 1
if n == 1:
return 1 # Base Case 2
return fibonacci(n - 1) + fibonacci(n - 2) # Recursive Case
print(fibonacci(6)) # Output: 8
3.Reverse a String
def reverse_string(s):
if len(s) == 0:
return s # Base Case
return s[-1] + reverse_string(s[:-1]) # Recursive Case
print(reverse_string("hello")) # Output: "olleh"
4. Tower of Hanoi
def tower_of_hanoi(n, source, target, auxiliary):
if n == 1:
print(f"Move disk 1 from {source} to {target}")
return
tower_of_hanoi(n - 1, source, auxiliary, target)
print(f"Move disk {n} from {source} to {target}")
tower_of_hanoi(n - 1, auxiliary, target, source)
tower_of_hanoi(3, 'A', 'C', 'B')
Advantages and Disadvantages of Recursion in Python
Advantages:
- Simplifies complex problems.
- Reduces code length and improves readability.
Disadvantages:
- May lead to stack overflow if the recursion depth is too high.
- Generally slower compared to iterative solutions due to function call overhead.
Tips for Writing Recursive Functions
- Identify the Base Case: Ensure your recursion terminates to avoid infinite loops.
- Optimize with Memoization: Use caching techniques to store intermediate results and prevent repeated calculations.
- Test Edge Cases: Handle special inputs like negative numbers, zero, or large inputs.
Recursion vs. Iteration
While recursion can make code cleaner, iteration (using loops) is often more efficient. Choose recursion for problems that naturally fit the divide-and-conquer approach.
Conclusion
Recursion is a powerful concept that simplifies solving problems with repetitive tasks or patterns. By mastering recursion, you’ll unlock new ways to approach coding challenges and stand out in technical interviews.
INTERVIEW QUESTIONS
1. Find the Factorial of a Number Using Recursion in Python
Company: Amazon
Answer:The factorial of a number n is defined as the product of all positive integers less than or equal to n. It can be computed using recursion where the base case is when n = 1 and the recursive case multiplies n with the factorial of n-1.
def factorial(n):
if n == 0 or n == 1: # Base Case
return 1
return n * factorial(n - 1) # Recursive Case
print(factorial(5)) # Output: 120
2. Calculate the nth Fibonacci Number Using Recursion in Python
Company: Google
Answer:
The Fibonacci sequence is defined as F(0) = 0, F(1) = 1, and for n >= 2, F(n) = F(n-1) + F(n-2). This problem uses recursion to calculate the nth Fibonacci number.
def fibonacci(n):
if n <= 1: # Base Case
return n
return fibonacci(n - 1) + fibonacci(n - 2) # Recursive Case
print(fibonacci(6)) # Output: 8
3. Implement the Tower of Hanoi Problem
Company: Microsoft
Answer:
The Tower of Hanoi is a classic problem in recursion. It involves moving disks from one rod to another while adhering to specific rules. The recursive solution involves moving n-1 disks to an auxiliary rod and then moving the nth disk to the target rod.
def tower_of_hanoi(n, source, target, auxiliary):
if n == 1: # Base Case
print(f"Move disk 1 from {source} to {target}")
return
tower_of_hanoi(n - 1, source, auxiliary, target) # Move n-1 disks to auxiliary
print(f"Move disk {n} from {source} to {target}") # Move nth disk to target
tower_of_hanoi(n - 1, auxiliary, target, source) # Move n-1 disks from auxiliary to target
tower_of_hanoi(3, 'A', 'C', 'B') # Output: Steps to solve Tower of Hanoi with 3 disks
4. Reverse a String Using Recursion in Python
Company: Infosys
Answer:
This function recursively reverses a string by taking the last character of the string and combining it with the result of recursively calling the function on the rest of the string.
def reverse_string(s):
if len(s) == 0: # Base Case
return s
return s[-1] + reverse_string(s[:-1]) # Recursive Case
print(reverse_string("hello")) # Output: "olleh"
5. Check if a Number is a Palindrome Using Recursion
Company: TCS
Answer:
This function checks if a string is a palindrome by comparing the first and last characters. If they are equal, the function recursively checks the substring without the first and last characters. If at any point the characters do not match, it returns False.
def is_palindrome(s):
if len(s) <= 1: # Base Case
return True
if s[0] != s[-1]:
return False
return is_palindrome(s[1:-1]) # Recursive Case
print(is_palindrome("madam")) # Output: True
QUIZZES
Recursion in python quiz
Question
Your answer:
Correct answer:
Your Answers
